Simulations
A simulation is the use of a computer software to represent the dynamic responses of one system by the behaviour of another system modeled after it. A simulation uses a mathematical descriptions, or models, of a real system in the form of a computer program.

College Board Essential Knowledge
Simulation are absractions of more complex objects or phenomena for a specific purpose
- Mimic Real World Events
- Allows investigation of phenomenons without contraints of the Real World
- Helps you draw accurate inferences
Simulations utilize varying sets of values to reflect the changings states of a phenomenon
- simulations can simplfly things for functionality
- Simulations can contain bias from real world elements, that were chosen to be included or excluded
Simulations work best when the real world experemnts are too impractical or time consuming. For example, simulating how different cars behave when they crash, would be much better than crashng actual cars in the real world, which would be expensive and dangerous.
Rolling the Dice
Simulating something like a dice roll in real life would require accounting for things like: weight, flaws in design, thrust, and gravity.
- KEEP IT SIMPLE! just use a random-number generator! Ignore minor causes of variablility
Random
- “Random” is a built-in python function that allow the user to draw a random value from a set range.
- A Random Number Generator (RNG) is a common simulation that selects a random value from an array.
- The following code cell utilizes “random” to select a number from 1 to 100.
#imports random module so we can use it in our code
import random
#sets variable random_number as a random number between 1 and 100
random_number = random.randint(1, 100)
#Printing out your random Number
print(random_number)
More complex usage of “random”; Coin Toss Simulation
import random
def flip_coin():
return random.choice(["Heads", "Tails"])
def coin_flip_simulation(num_flips):
heads_count = 0
tails_count = 0
for _ in range(num_flips):
result = flip_coin()
if result == "Heads":
heads_count += 1
else:
tails_count += 1
return heads_count, tails_count
if __name__ == "__main__":
num_flips = 1000 #This is the number of coin flips you want to simulate
heads, tails = coin_flip_simulation(num_flips)
print("Number of Heads: "+ str(heads))
print("Number of Tails: " + str(tails))
print("Heads Probability: "+ str({heads / num_flips}))
print("Tails Probability: "+ str({tails / num_flips}))
Number of Heads: 508
Number of Tails: 492
Heads Probability: {0.508}
Tails Probability: {0.492}
Popcorn Hack #1
Utilize “random” to create a basic simulation of a rolling TWO dice. Print the sum of both dice rolls. Remember to practice good syntax when naming your variables.
import random
roll1 = random.choice(1, 6)
roll2 = random.choice(1, 6)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
/tmp/ipykernel_2469/3028805664.py in <module>
1 import random
2
----> 3 roll1 = random.choice(1, 6)
4 roll2 = random.choice(1, 6)
5
TypeError: Random.choice() takes 2 positional arguments but 3 were given
Algorithms
Simulations often utilize algorithms and equations to perform tasks because simulations don’t always have the same output
- the output of a simulation depends on the input
An algorithm is a finite sequence of instructions used to solve problems or perform computations.
- commonly used alongside functions
Example Algorithm in a function
#Defining Function
def algorithm(input):
#Manipulating input and preparing it for the output.
output = input+2
#Return the output
return output
#Call the Function to start the algorithm
algorithm(5)
7
Mathematics
- Math can also prove to be very useful in certain types of situations.
- Commonly used along with Algorithms when simulating various things
Popcorn Hack #2
Simulate how long an object will fall for using an algorithm, with user-inputed variables for height dropped. Use the following formula as a reference.
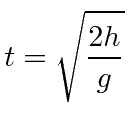
- t = time (output)
- h = height dropped from (input)
- g = constant (given)
# Constant, Acceleration due to gravity (m/s^2)
G = 9.81
def simulation(height_dropped):
h = input("Enter number")
t = (2 * h / G ) ** 2
print(t)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
/tmp/ipykernel_2469/2066765890.py in <module>
6 t = (2 * h / G ) ** 2
7
----> 8 print(t)
NameError: name 't' is not defined
Using Loops in Simulations
For loops can also be used in simulations
- They can simulate events that repeat but don’t always have the same output
# Example For Loop
#Creating For Loop to repeat 4 times
for i in range(4):
#Action that happens inside for loop
print("This is run number: " + str(i))
This is run number: 0
This is run number: 1
This is run number: 2
This is run number: 3
Popcorn Hack #3
You are gambling addict (sigma).
Each session you roll 2 dice.
If your dice roll is greater than or equal to 9 you win the session.
If you win over 5 sessions, you win the jackpot.
Simulate your odds to predict if you will hit the jackpot (how many rounds did you win?) using a for loop and random.
# Code Code Code
import random
wins = 0
for i in range(9):
num = random.randint(0,6) + random.randint(0,6)
if(num >= 9):
wins+=1
print(wins)
if(wins >= 5):
print("YOU WIN")
2
BONUS POPCORN HACK
Welcome to Flight Simulator! Your goal is to complete a Python program that simulates a flight We’ve set up some initial values for altitude, speed, and fuel. Your task is to update these values to make the flight more realistic.
- Your mission:
- Use random changes to simulate altitude, speed, and fuel changes.
- Keep the flight going until it reaches 10,000 feet or runs out of fuel.
- Make sure altitude, speed, and fuel remain realistic.
import random
# Initial parameters
altitude = 0
speed = 0
fuel = 100
print("Welcome to Flight Simulator!")
# Code Code Code
QUIZ TIME
- Quick true or false quiz, whoever answers this correctly(raise your hand) gets a piece of gum or a dinero.
T or F
- A simulation will always have the same result. T or F
- A simulation investigates a phenomenom without real-world constraints of time, money, or safety. T or F
- A simulation has results which are more accurate than an experiment, T or F
- A simulation can model real-worl events that are not practical for experiments
HOMEWORK HACK #1
First finish Popcorn Hack #3. Expand the simulation to involve your own money.
starting money: $100
(Dice Roll <= 3) → lose $70
( 6> Dice Roll >3) → lose $40
( 9> Dice Roll >=6) → win $20
( Dice Roll>= 9 + Session Win) → win $50
Jackpot → win $100
import random
money = 100
session_wins = 0
for i in range(9):
dice1 = random.randint(1, 6)
dice2 = random.randint(1, 6)
print("You rolled a " + str(dice1 + dice2) + "!")
if dice1 + dice2 <= 3:
print("Lose $70!")
money = money - 70
elif dice1 + dice2 < 6:
print("Lose $40!")
money = money - 40
elif dice1 + dice2 < 9:
print("Win $20!")
money = money + 20
session_wins = session_wins + 1
else:
print("Win $50!")
money = money + 50
session_wins = session_wins + 1
if session_wins == 5:
print("You won the jackpot!")
money = money + 100
print(f"Your total money is {money}")
You rolled a 8!
Win $20!
You rolled a 10!
Win $50!
You rolled a 2!
Lose $70!
You rolled a 9!
Win $50!
You rolled a 5!
Lose $40!
You rolled a 5!
Lose $40!
You rolled a 6!
Win $20!
You rolled a 8!
Win $20!
You won the jackpot!
You rolled a 8!
Win $20!
Your total money is 230
HOMEWORK HACK #2
Given initial parameters for a car simulation, including its initial speed, acceleration rate, deceleration rate, maximum speed, and initial distance, write a program to simulate the car’s journey and determine the final speed, distance covered, and time taken before it either covers 1000 meters or slows down to below 5 m/s?
# Initial parameters
speed = 0 # Initial speed
acceleration = 2 # Acceleration rate in m/s^2
deceleration = 1 # Deceleration rate in m/s^2
max_speed = 60 # Maximum speed in m/s
distance = 0 # Initial distance
time = 0 # Initial time
import random
while (distance < 1000) or (speed < 5):
acceleration = random.randint(0, 4)
deceleration = random.randint(0, 4)
if acceleration > deceleration:
speed += (acceleration - deceleration)
else:
speed -= (deceleration - acceleration)
if speed > max_speed:
speed = max_speed
distance += speed
time += 1
print(f"Final Speed: {speed}")
print(f"Distance Covered: {distance}")
print(f"Time: {time}")
Final Speed: 17
Distance Covered: 1005
Time: 108

